Mục lục

1 Bảng công thức đạo hàm đầy đủ sơ cấp, cao cấp, lượng giác lớp 11, 12
2 Đạo hàm là nền tảng cốt lõi của giải tích (một nhánh toán học nghiên cứu sự thay đổi), giúp xác định tốc độ biến thiên của hàm số tại một điểm. Việc nắm vững bảng công thức đạo hàm và quy tắc tính là chìa khóa để giải quyết mọi bài toán từ cơ bản đến nâng cao!

Bảng công thức đạo hàm đầy đủ sơ cấp, cao cấp, lượng giác lớp 11, 12

1767944077 275 Bang cong thuc dao ham day du so cap cao — Bảng công thức đạo hàm đầy đủ sơ cấp, cao cấp, lượng giác lớp 11, 12

Để học tập và giải các bài toán đạo hàm hiệu quả, xem ngay các mẫu laptop cho học sinh, sinh viên giá tốt:

Đạo hàm là nền tảng cốt lõi của giải tích (một nhánh toán học nghiên cứu sự thay đổi), giúp xác định tốc độ biến thiên của hàm số tại một điểm. Việc nắm vững bảng công thức đạo hàm và quy tắc tính là chìa khóa để giải quyết mọi bài toán từ cơ bản đến nâng cao!

1. Đạo hàm là gì?

Đạo hàm là một khái niệm toán học đo lường tốc độ thay đổi tức thời của một hàm số tại một điểm cụ thể, biểu thị qua độ dốc của tiếp tuyến với đồ thị hàm số tại điểm đó.

Đạo hàm còn là tỉ số giữa sự thay đổi của hàm số và sự thay đổi của biến số, có ứng dụng rộng rãi trong vật lý (vận tốc, gia tốc) và nhiều lĩnh vực khoa học khác để phân tích sự biến thiên.

2. Các quy tắc tính đạo hàm

Trong thực tế, hàm số thường là sự kết hợp phức tạp của nhiều thành phần. Để tính đạo hàm của chúng, bạn cần tuân theo các quy tắc đại số cơ bản sau đây:

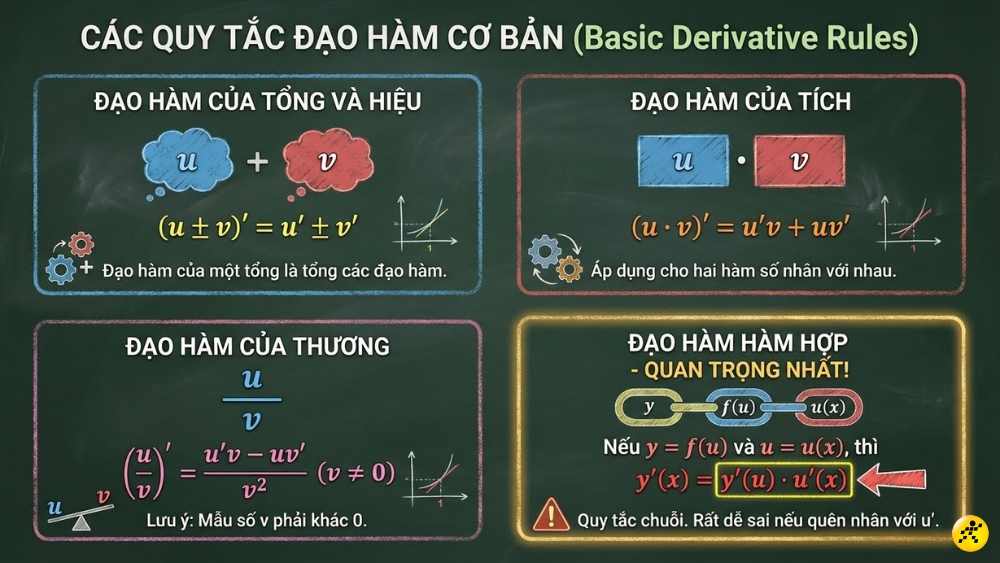
Quy tắc tính đạo hàm

➕ Đạo hàm của tổng và hiệu: (u ± v)’ = u’ ± v’. Đạo hàm của một tổng bằng tổng các đạo hàm.
✖️ Đạo hàm của một tích: (u · v)’ = u’v + uv’.
➗ Đạo hàm của một thương: (u/v)’ = (u’v – uv’)/v² (v ≠ 0).

⚠️ QUY TẮC CHUỖI (HÀM HỢP): Nếu y = f(u) và u = u(x), thì y'(x) = y'(u) · u'(x).

Đây là quy tắc quan trọng nhất và rất dễ sai sót nếu bạn quên nhân thêm u’.

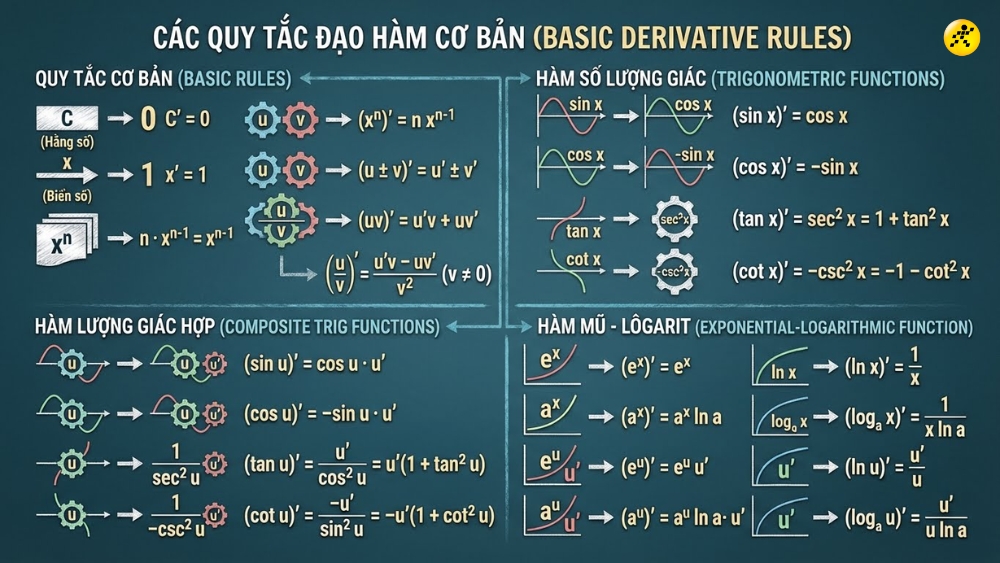
3. Công thức đạo hàm sơ cấp

Dưới đây là bảng tổng hợp đầy đủ, với c là hằng số và các hàm lượng giác ở đơn vị radian.

Loại hàm số	Bảng công thức chi tiết
Quy tắc cơ bản	C’ = 0 x’ = 1 (xⁿ)’ = nx^n-1 (u/v)’ = (u’v – uv’)/v²
Hàm lượng giác	(sin x)’ = cos x (cos x)’ = -sin x (tan x)’ = sec²x (cot x)’ = -csc²x
Hợp lượng giác	(sin u)’ = cos u · u’ (cos u)’ = -sin u · u’ (tan u)’ = (u'(1 + tan²u))/cos²u
Mũ – Logarit	(e^x)’ = e^x (a^x)’ = a^xln a (ln x)’ = 1/x (log_ax)’ = 1/(x ln a)

Công thức đạo hàm sơ cấp

Hàm mũ-logarit hợp bổ sung

(e^u)’ = e^uu’
(a^u)’ = a^uln a · u’
(ln u)’ = u’/u
(log_au)’ = u’/(u ln a)

Đạo hàm phân thức hữu tỉ đặc biệt

🚀 (1/x)’ = -1/x²
🚀 (1/u)’ = -u’/u²
🚀 ((ax+b)/(cx+d))’ = (ad – bc)/(cx+d)²

4. Công thức đạo hàm cho lớp 11, 12

Công thức đạo hàm cho lớp 11

Công thức đạo hàm cho lớp 12

5. Công thức đạo hàm lượng giác

Công thức đạo hàm lượng giác

📚 Hệ thống đạo hàm lượng giác đầy đủ:

Đạo hàm cơ bản:

(sin x)’ = cos x
(cos x)’ = -sin x
(tan x)’ = sec²x
(cot x)’ = -csc²x
(sec x)’ = sec x tan x
(csc x)’ = -csc x cot x

Đạo hàm hàm hợp:

(sin u)’ = cos u · u’
(cos u)’ = -sin u · u’
(tan u)’ = u’/cos²u
(cot u)’ = -u’/sin²u
(sec u)’ = sec u tan u · u’

Đạo hàm lượng giác nghịch đảo:

(arcsin x)’ = 1/√(1-x²)
(arccos x)’ = -1/√(1-x²)
(arctan x)’ = 1/(1+x²)
(arccot x)’ = -1/(1+x²)

💡 Ví dụ minh họa lượng giác:

f(x) = sin(3x) → f'(x) = 3 cos(3x)
f(x) = tan(x²) → f'(x) = 2x sec²(x²)
f(x) = 1/cos x = sec x → f'(x) = sec x tan x
f(x) = sin(x/(x+1)) → f'(x) = cos(x/(x+1)) · 1/(x+1)²

📍 Mẹo ghi nhớ: Vòng tròn đạo hàm: sin → cos, cos → -sin, tan → sec². Vẽ đồ thị để hình dung tốc độ thay đổi.

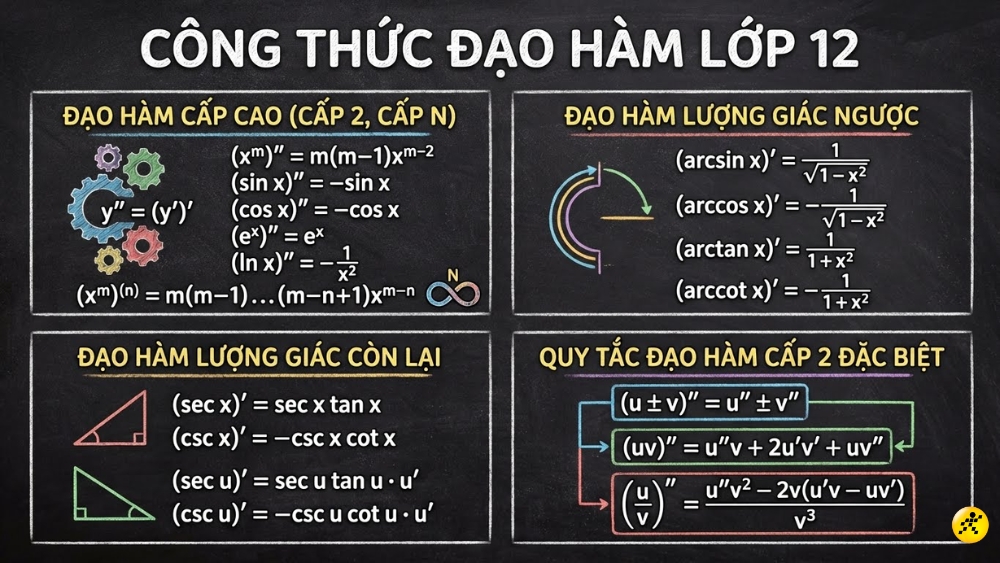
6. Công thức đạo hàm cấp cao

Công thức đạo hàm cấp cao

Định nghĩa: Đạo hàm cấp 2: y” = (y’)’ hoặc f”(x). Đạo hàm cấp n: f⁽ⁿ⁾(x) = [f^(n-1)(x)]’.

Đạo hàm cấp 2 các hàm cơ bản:

(x^m)” = m(m-1)x^m-2
(sin x)” = -sin x | (cos x)” = -cos x
(e^x)” = e^x | (ln x)” = -1/x²

Công thức tổng quát cấp n:

(x^m)⁽ⁿ⁾ = m(m-1)…(m-n+1)x^m-n
(sin x)⁽ⁿ⁾ = sin(x + nπ/2) | (cos x)⁽ⁿ⁾ = cos(x + nπ/2) | (e^x)⁽ⁿ⁾ = e^x

Quy tắc đạo hàm cấp 2 đặc biệt:

(u ± v)” = u” ± v”
(uv)” = u”v + 2u’v’ + uv”
(u/v)” = [u”v² – 2uv'(u’v – uv’)] / v³

7. Các dạng bài tập đạo hàm thường gặp

📝 Bài tập đạo hàm sơ cấp (Lớp 11)

Dạng 1.1: Đạo hàm đa thức & tổng/hiệu/tích

Bài tập: Tính f'(x) với f(x) = 2x³ – 5x² + 3x – 1.
Đáp án: f'(x) = 6x² – 10x + 3.
Cách giải: f'(x) = 3 · 2x² – 2 · 5x + 3 = 6x² – 10x + 3.

Dạng 1.2: Đạo hàm thương đơn giản

Bài tập: f(x) = (2x+1)/(x-1).
Đáp án: f'(x) = -3/(x-1)².
Cách giải: u=2x+1, u’=2; v=x-1, v’=1 → f'(x) = [2(x-1) – (2x+1) · 1]/(x-1)² = -3/(x-1)².

📚 Bài tập đạo hàm cao cấp (Lớp 12)

Dạng 2.1: Hàm hợp đa thức

Bài tập: f(x) = (x² + 3x – 2)⁴. Đáp án: f'(x) = 4(x² + 3x – 2)³ · (2x + 3).

Dạng 2.2: Đạo hàm mũ & logarit

Bài tập: y = e^√x + ln(x² + 1). Đáp án: y’ = e^√x/(2√x) + 2x/(x² + 1).

Dạng 2.3: Phân thức hữu tỉ

Bài tập: f(x) = x/(x+1). Đáp án: f'(x) = 1/(x+1)².

Dạng 2.4: Đạo hàm ẩn

Bài tập: xy + y² = x³. Đáp án: y’ = (3x² – y)/(x + 2y).

📐 Bài tập đạo hàm lượng giác (Lớp 12)

Dạng 3.1: Đạo hàm lượng giác cơ bản hợp

Bài tập: f(x) = sin(3x² + 1). Đáp án: f'(x) = cos(3x² + 1) · 6x.

Dạng 3.2: Đạo hàm tan, cot & biến đổi

Bài tập: y = √tan x. Đáp án: y’ = sec²x / (2√tan x).

Dạng 3.3: Tổng hợp lượng giác + hàm khác

Bài tập: f(x) = sin x / (e^x + cos x).

Đáp án: f'(x) = [cos x(e^x + cos x) – sin x(e^x – sin x)]/(e^x + cos x)².

💡 Lộ trình luyện tập hiệu quả: Tuần 1: Sơ cấp (50 bài) | Tuần 2: Cao cấp (70 bài) | Tuần 3: Lượng giác + Thi THPT (100 bài).

8. Ứng dụng của đạo hàm trong học tập và thực tế

Đạo hàm không chỉ là lý thuyết mà còn là công cụ giải quyết nhiều vấn đề thực tiễn:

📈 Toán học lớp 12: Khảo sát sự biến thiên, tìm cực trị, vẽ đồ thị hàm số.
⚡ Vật lý: Xác định vận tốc và gia tốc tức thời.
💰 Kinh tế & Công nghệ: Tính chi phí biên, tối ưu hóa thuật toán AI.

🛒 GỢI Ý DÀNH CHO BẠN

MacBook Air – Với màn hình Retina sắc nét trên laptop và các dòng chip M2, M3, M4 mạnh mẽ, đây là công cụ hỗ trợ tuyệt vời để học sinh, sinh viên chạy mượt mà các phần mềm vẽ đồ thị hàm số và giải toán đạo hàm trực tuyến.

>> Mua ngay MacBook Air tại TGDĐ

9. Câu hỏi liên quan

❓ Câu hỏi thường gặp

Làm thế nào để nhớ hết bảng công thức đạo hàm?

Bạn nên thực hành làm nhiều bài tập thay vì chỉ học vẹt. Ngoài ra, việc sử dụng các mẹo lượng giác và tự kẻ bảng tóm tắt dán tại góc học tập rất hiệu quả.

Đạo hàm và vi phân khác nhau như thế nào?

Đạo hàm là tốc độ thay đổi của hàm số, trong khi vi phân (dy = f'(x)dx) biểu thị sự thay đổi tuyệt đối cực nhỏ của hàm số đó.

Tại sao hàm số liên tục chưa chắc có đạo hàm?

Tại một điểm đồ thị bị “gãy” hoặc “nhọn” (ví dụ hàm trị tuyệt đối tại x=0), tiếp tuyến không duy nhất nên không tồn tại đạo hàm.

Có thể dùng máy tính cầm tay để tính đạo hàm không?

Có, hầu hết các dòng máy tính khoa học hiện nay đều hỗ trợ phím tính giá trị đạo hàm tại một điểm cụ thể.

Xem thêm các mẫu laptop GIẢM SỐC đang kinh doanh tại Thế Giới Di Động:

🔗

Xem thêm kiến thức bổ trợ:

Hy vọng bảng công thức và các quy tắc trên đã cung cấp cho bạn kiến thức hữu ích. Hãy chăm chỉ luyện tập để đạt kết quả cao nhất nhé!

TIN TỨC – konicahanoi
Nguồn tham khảo