Mục lục
- 1 Bảng tổng hợp công thức lượng giác đầy đủ, dễ nhớ cho học sinh
- 2 Công thức lượng giác là nền tảng quan trọng trong chương trình Toán học, đặc biệt là lớp 10 và 11. Việc nắm vững các công thức này không chỉ giúp giải quyết bài tập mà còn là công cụ đắc lực khi ôn luyện trên laptop. Cùng xem ngay bài viết để hệ thống kiến thức nhé!
- 2.1 1. Công thức lượng giác cơ bản
- 2.2 2. Công thức lượng giác các cung liên kết
- 2.3 3. Công thức lượng giác cộng, trừ
- 2.4 4. Công thức lượng giác nhân đôi, nhân ba
- 2.5 5. Công thức lượng giác hạ bậc
- 2.6 6. Công thức lượng giác tổng thành tích
- 2.7 7. Công thức lượng giác tích thành tổng
- 2.8 8. Các dạng bài tập lượng giác thường gặp
- 2.9 9. Câu hỏi liên quan
Bảng tổng hợp công thức lượng giác đầy đủ, dễ nhớ cho học sinh





Dưới đây là đoạn source đã được xử lý toàn bộ các công thức toán học từ LaTeX sang HTML và decode thực thể HTML theo đúng guideline bạn cung cấp:
Laptop cấu hình đỉnh – Tra cứu công thức thần tốc tại TGDĐ:Công thức lượng giác là nền tảng quan trọng trong chương trình Toán học, đặc biệt là lớp 10 và 11. Việc nắm vững các công thức này không chỉ giúp giải quyết bài tập mà còn là công cụ đắc lực khi ôn luyện trên laptop. Cùng xem ngay bài viết để hệ thống kiến thức nhé!
1. Công thức lượng giác cơ bản
Trong lượng giác học, đây là nhóm công thức cốt lõi nhất, được suy ra từ định nghĩa hàm số sin cos tan cot trên đường tròn đơn vị (bán kính R=1). Các hệ thức này là nền tảng để biến đổi mọi đẳng thức phức tạp hơn.

Công thức lượng giác cơ bản
- sin2 α + cos2 α = 1
- tan α = sin α / cos α (cos α ≠ 0)
- cot α = cos α / sin α (sin α ≠ 0)
- tan α · cot α = 1
- 1 + tan2 α = sec2 α = 1 / cos2 α
- 1 + cot2 α = csc2 α = 1 / sin2 α
2. Công thức lượng giác các cung liên kết
Nhóm công thức cung liên kết giúp đơn giản hóa các biểu thức chứa góc phức tạp bằng cách đưa về các góc trong góc phần tư thứ nhất.

Công thức lượng giác các cung liên kết
💡 MẸO NHỚ: cos đối, sin bù, phụ chéo, hơn kém π tan cot
1️⃣ Cung đối nhau (x, -x)
- cos(-x) = cos x
- sin(-x) = -sin x
- tan(-x) = -tan x
- cot(-x) = -cot x
2️⃣ Cung bù nhau (x, π-x)
- sin(π-x) = sin x
- cos(π-x) = -cos x
- tan(π-x) = -tan x
- cot(π-x) = -cot x
3️⃣ Cung phụ nhau (x, π/2-x)
- sin(π/2-x) = cos x
- cos(π/2-x) = sin x
- tan(π/2-x) = cot x
- cot(π/2-x) = tan x
4️⃣ Hơn kém π (x ± π)
- sin(x ± π) = -sin x
- cos(x ± π) = -cos x
- tan(x ± π) = tan x
- cot(x ± π) = cot x
5️⃣ Hơn π/2 (π/2+x)
- sin(π/2+x) = cos x
- cos(π/2+x) = -sin x
- tan(π/2+x) = -cot x
- cot(π/2+x) = -tan x
3. Công thức lượng giác cộng, trừ
Công thức cộng là công cụ mạnh mẽ để khai triển các biểu thức lượng giác của mọi tổng hoặc hiệu hai góc. Việc sử dụng thành thạo nhóm này giúp bạn giải quyết nhanh các bài toán biến đổi phức tạp.

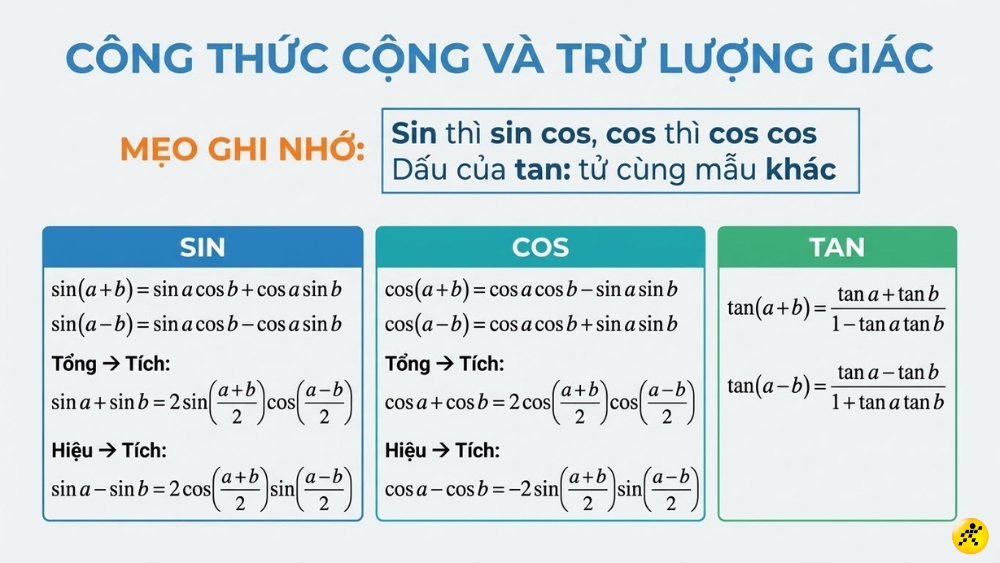
Công thức lượng giác cộng, trừ
💡 MẸO NHỚ: Sin cộng sin cos, cos cộng cos cos
SIN
- sin(a+b) = sin a cos b + cos a sin b
- sin(a-b) = sin a cos b – cos a sin b
- Tổng → Tích: sin a + sin b = 2 sin((a+b)/2) cos((a-b)/2)
- Trừ → Tích: sin a – sin b = 2 cos((a+b)/2) sin((a-b)/2)
COS
- cos(a+b) = cos a cos b – sin a sin b
- cos(a-b) = cos a cos b + sin a sin b
- Tổng → Tích: cos a + cos b = 2 cos((a+b)/2) cos((a-b)/2)
- Trừ → Tích: cos a – cos b = -2 sin((a+b)/2) sin((a-b)/2)
- tan(a+b) = (tan a + tan b)/(1 – tan a tan b)
- tan(a-b) = (tan a – tan b)/(1 + tan a tan b)
📝 THƠ NHỚ NHANH:
SIN cộng sin cos, COS cộng cos cosCOS trừ cos SIN, SIN trừ cos SINSin sin âm nửa cos cộng trừCos cos nửa cos cộng bớt
4. Công thức lượng giác nhân đôi, nhân ba
Nhóm công thức nhân thực chất là hệ quả của công thức cộng khi ta đặt hai góc bằng nhau (a = b). Chúng giúp biểu diễn góc bội qua góc đơn.

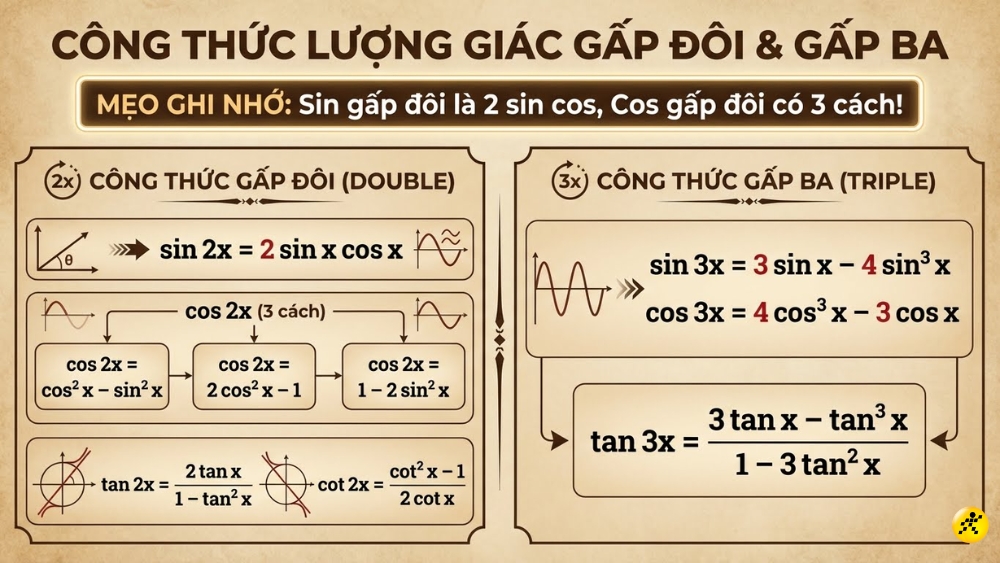
Công thức lượng giác nhân đôi, nhân ba
💡 MẸO NHỚ: Sin đôi 2sin cos, Cos đôi 3 kiểu!
SIN
- sin 2x = 2 sin x cos x
- sin 3x = 3 sin x – 4 sin3 x
COS (3 dạng)
- cos 2x = cos2 x – sin2 x
- cos 2x = 2 cos2 x – 1
- cos 2x = 1 – 2 sin2 x
TAN
- tan 2x = 2 tan x / (1 – tan2 x)
- tan 3x = (3 tan x – tan3 x) / (1 – 3 tan2 x)
COTAN
- cot 2x = (cot2 x – 1) / (2 cot x)
- cos 3x = 4 cos3 x – 3 cos x
📝 THƠ NHỚ SIÊU NHANH:
SIN ĐÔI: 2 sin cosCOS ĐÔI: cos cos trừ sin sin hoặc 2 cos bình – 1 hoặc 1 – 2 sin bìnhSIN BA: 3 sin – 4 sin mũ baCOS BA: 4 cos mũ ba – 3 cosTAN ĐÔI: 2 tan trên 1 trừ tan bình
🔄 CHUYỂN ĐỔI NHANH:
- cos 2x = 2 cos2 x – 1 = 1 – 2 sin2 x
- sin 2x = 2 sin x cos x = 2 tan x / sec2 x
5. Công thức lượng giác hạ bậc
Công thức hạ bậc thường được dùng để giảm bậc của các biểu thức lượng giác, cực kỳ hữu dụng khi tính tích phân hàm lượng giác hoặc giải phương trình bậc cao.

Công thức lượng giác hạ bậc
💡 MẸO NHỚ: Sin bình nửa trừ cos đôi, Cos bình nửa cộng cos đôi
🔹 BẬC 2 (CƠ BẢN)
- sin2 x = (1 – cos 2x)/2
- cos2 x = (1 + cos 2x)/2
- tan2 x = (1 – cos 2x)/(1 + cos 2x)
- cot2 x = (1 + cos 2x)/(1 – cos 2x)
🔹 BẬC 3 (QUAN TRỌNG)
- sin3 x = (3 sin x – sin 3x)/4
- cos3 x = (3 cos x + cos 3x)/4
- tan3 x = (3 tan x – tan3 x)/(1 – 3 tan2 x)
🔹 BẬC 4
- sin4 x = (3 – 4 cos 2x + cos 4x)/8
- cos4 x = (3 + 4 cos 2x + cos 4x)/8
- sin2 x cos2 x = (1 – cos 4x)/8
🔹 BIẾN ĐỔI HAY DÙNG
- sin2 x + cos2 x = 1
- sin4 x + cos4 x = (1 + 2 cos2 2x)/2
- 1 + tan2 x = sec2 x
📝 THƠ NHỚ SIÊU NHANH:
BẬC 2: Sin bình = (1-trừ)/2; Cos bình = (1+cộng)/2BẬC 3: Sin mũ ba = (3sin-trừ)/4; Cos mũ ba = (3cos+cộng)/4BẬC 4: Sin bốn = (3-trừ 4cos+cộng)/8
⚡ MẸO ÁP DỤNG:
- Bước 1: Dùng sin2+cos2=1 → hạ bậc 2
- Bước 2: sin3, cos3 → công thức bậc 3
- Bước 3: sin4 = (sin2)2 → hạ 2 lần
6. Công thức lượng giác tổng thành tích
Khi đối mặt với phương trình lượng giác dạng tổng, việc biến đổi về dạng tích giúp bạn tìm ra nghiệm dễ dàng hơn bằng cách giải từng nhân tử riêng biệt.

Công thức lượng giác tổng thành tích
💡 MẸO NHỚ: Cộng cos sin → cos cos, Trừ cos sin → sin sin
SIN
- sin a + sin b = 2 sin((a+b)/2) cos((a-b)/2)
- sin a – sin b = 2 cos((a+b)/2) sin((a-b)/2)
COS
- cos a + cos b = 2 cos((a+b)/2) cos((a-b)/2)
- cos a – cos b = -2 sin((a+b)/2) sin((a-b)/2)
📝 THƠ NHỚ SIÊU NHANH:
SIN + SIN = 2 SIN trung bình COS chênh lệchSIN – SIN = 2 COS trung bình SIN chênh lệchCOS + COS = 2 COS trung bình COS chênh lệchCOS – COS = TRỪ 2 SIN trung bình SIN chênh lệch
⚡ Ví dụ minh họa:
Chứng minh: sin 75° + sin 15° = 1Áp dụng: sin A + sin B = 2 sin((75+15)/2) cos((75-15)/2) = 2 sin 45° cos 30° = 2 · (√2/2) · (√3/2) ≈ 1 ✓
✅ ỨNG DỤNG THI THPTQG:
- Giản hóa sin(x+α) + sin(x-α)
- Chứng minh đẳng thức lượng giác
- Giải phương trình sin x + sin 3x = 0
- Tính giá trị sin 75° ± sin 15°
7. Công thức lượng giác tích thành tổng
Nhóm công thức này là quá trình ngược lại của tổng thành tích, được sử dụng phổ biến trong các bài toán tìm nguyên hàm và tính tích phân lượng giác.

Công thức lượng giác tích thành tổng
💡 MẸO NHỚ: Sin sin âm cos cos, Sin cos cộng sin sin
SIN×SIN & COS×COS
- sin a sin b = [-cos(a+b) + cos(a-b)] / 2
- cos a cos b = [cos(a+b) + cos(a-b)] / 2
SIN×COS & COS×SIN
- sin a cos b = [sin(a+b) + sin(a-b)] / 2
- cos a sin b = [sin(a+b) – sin(a-b)] / 2
📝 THƠ NHỚ SIÊU NHANH:
SIN SIN = ÂM NỬA cos cộng trừCOS COS = NỬA cos cộng trừSIN COS = NỬA sin cộng trừCOS SIN = NỬA sin cộng bớt
⚡ Ví dụ minh họa:
Tính: sin 75° cos 15°→ sin A cos B = [sin(75+15) + sin(75-15)] / 2 = [sin 90° + sin 60°] / 2 = (1 + √3/2) / 2 = (2 + √3)/4 ✓
🔄 LIÊN HỆ: Ngược lại với Tổng → Tích
8. Các dạng bài tập lượng giác thường gặp

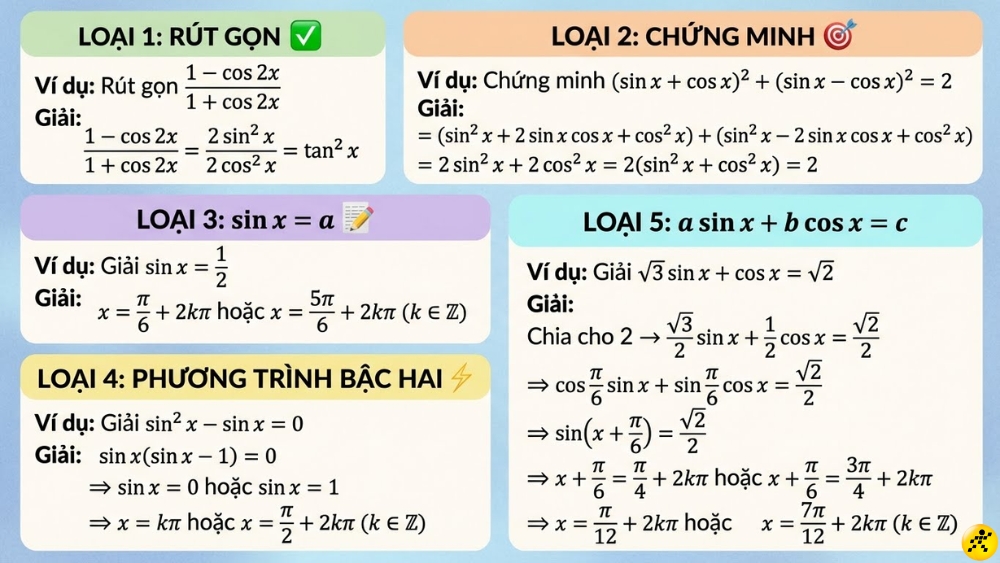
Các dạng bài tập lượng giác thường gặp
📐 DẠNG 1: RÚT GỌN
Ví dụ: Rút gọn (1 – cos 2x)/(1 + cos 2x)
Giải: (1 – cos 2x)/(1 + cos 2x) = [2 sin2 x]/[2 cos2 x] = tan2 x ✓
✅ DẠNG 2: CHỨNG MINH
Ví dụ: (sin x + cos x)2 + (sin x – cos x)2 = 2
Giải: = sin2 x + 2 sin x cos x + cos2 x + sin2 x – 2 sin x cos x + cos2 x = 2(sin2 x + cos2 x) = 2 ✓
🎯 DẠNG 3: sin x = a
Ví dụ: Giải sin x = 1/2
Nghiệm: x = π/6 + 2kπ hoặc x = 5π/6 + 2kπ (k ∈ Z)
📝 DẠNG 4: PT BẬC 2
Ví dụ: sin2 x – sin x = 0
Giải: sin x(sin x – 1) = 0 ⇒ x = kπ hoặc x = π/2 + 2kπ
⚡ DẠNG 5: a sin x + b cos x = c
Ví dụ: √3 sin x + cos x = √2
Giải: Chia cho 2 → sin(x + π/6) = √2/2 ⇒ x + π/6 = π/4 + 2kπ hoặc 3π/4 + 2kπ
🚀 MẸO LÀM BÀI NHANH:
- PT cơ bản: Nhớ chính xác nghiệm sin/cos đặc biệt.
- Dạng 5: Luôn chia cho R = √(a2 + b2).
- Rút gọn: Dùng sin2 + cos2 = 1 hoặc nhân đôi.
🛒 GỢI Ý DÀNH CHO BẠN
Laptop Acer Swift Go 14 – Thiết kế mỏng nhẹ, pin cực trâu kết hợp màn hình OLED sắc nét, giúp bạn tra cứu công thức và học online mượt mà suốt cả ngày dài. Sắm ngay tại TGDĐ
9. Câu hỏi liên quan
❓Công thức lượng giác được áp dụng thực tế ở đây?
Lượng giác được áp dụng rộng rãi trong đo đạc địa lý, kỹ thuật xây dựng, hàng hải và vật lý sóng.
❓ Làm thế nào để nhớ hết lượng công thức này?
Hãy học theo logic nhóm, làm bài tập thường xuyên và sử dụng các mẹo thơ nhớ nhanh trong bài viết.
❓ Có phần mềm này giúp học công thức lượng giác không?
Có, các phần mềm như GeoGebra hoặc Symbolab giúp trực quan hóa và kiểm tra công thức cực nhanh.
🔗
Tham khảo thêm các bài viết:
Hy vọng bài viết này đã giúp bạn hệ thống lại kiến thức quan trọng để học tập hiệu quả. Hẹn gặp lại bạn trong các bài chia sẻ tiếp theo!




