Để học tập và tra cứu kiến thức toán học hiệu quả, xem ngay các mẫu điện thoại giá tốt:

Trong toán học, tập hợp Z đóng vai trò là nền tảng quan trọng giúp mở rộng hệ thống số từ các số tự nhiên cơ bản sang các giá trị âm. Việc hiểu rõ Z là tập hợp số gì không chỉ giúp bạn giải quyết các bài toán lớp 6 mà còn ứng dụng linh hoạt trong đời sống. Hãy cùng khám phá ngay nhé!

1. Z là tập hợp số gì?

Trong chương trình toán học phổ thông, ký hiệu Z là tập hợp số nguyên (integers). Tên gọi này bao quát các số tự nhiên dương, các số đối của chúng (số nguyên âm) và số 0. Một điểm thú vị về vị lịch sử là ký hiệu Z bắt nguồn từ từ “Zahlen” trong tiếng Đức, có nghĩa là “số”.

Tập hợp số nguyên Z được định nghĩa bao gồm các phần tử không có phần thập phân. Bạn có thể hình dung tập hợp này dưới dạng liệt kê như sau:

Z = {…, -4, -3, -2, -1, 0, 1, 2, 3, 4, …}

Đặc điểm của tập hợp Z là tính vô hạn về cả hai phía. Nghĩa là, không có số nguyên nào là nhỏ nhất và cũng không có số nguyên nào là lớn nhất. Khoảng cách giữa hai phần tử liên tiếp trong tập hợp luôn bằng 1 đơn vị.

Z là tập hợp số nguyên

2. Các thành phần và tập hợp con của Z

Để thuận tiện trong việc tính toán và phân loại, các nhà toán học chia tập hợp số nguyên Z thành ba nhóm thành phần chính. Việc nắm vững các tập hợp con này sẽ giúp học sinh tránh được những nhầm lẫn phổ biến.

Cụ thể các thành phần của tập hợp Z bao gồm:

• Số nguyên dương (Z+): Bao gồm các số nguyên lớn hơn 0 như 1, 2, 3… Đây thực chất chính là tập hợp số tự nhiên khác 0 (ký hiệu là N*).
• Số nguyên âm (Z-): Bao gồm các số nguyên nhỏ hơn 0, có dấu trừ đứng trước như -1, -2, -3… Đây là các số đối của số nguyên dương.
• Số 0: Là một phần tử đặc biệt trong tập hợp Z. Số 0 là số nguyên nhưng không phải là số nguyên dương và cũng không phải là số nguyên âm.
• Số nguyên khác 0 (Z*): Đây là tập hợp con của Z bao gồm tất cả các số nguyên ngoại trừ số 0.

Các thành phần và tập hợp con của Z

Bảng tóm tắt các tập hợp con thường gặp:

Tên gọi	Ký hiệu	Ví dụ phần tử
Số nguyên dương	Z+	1, 5, 10, 100
Số nguyên âm	Z-	-1, -5, -10, -100
Số nguyên khác 0	Z*	{…, -2, -1, 1, 2, …}

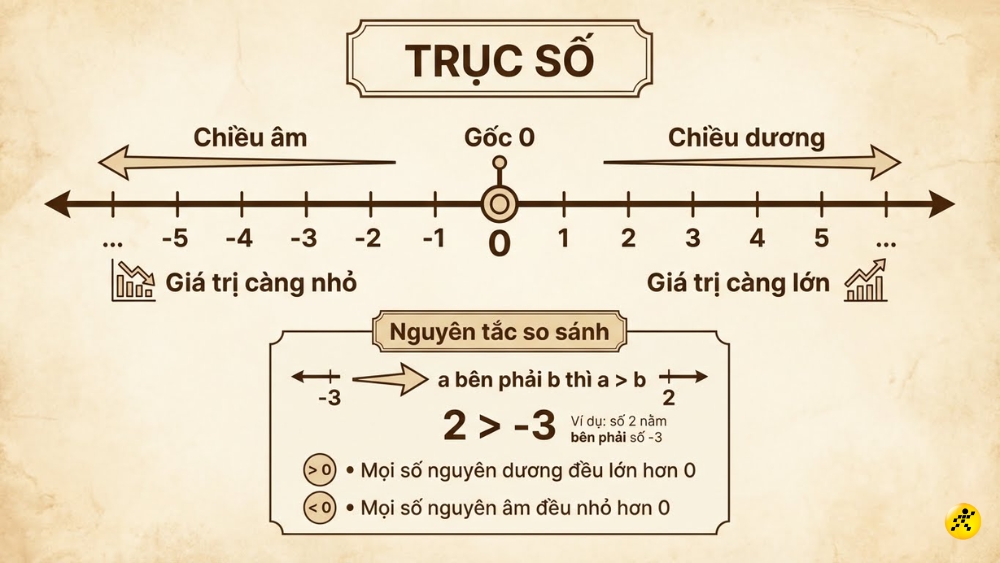
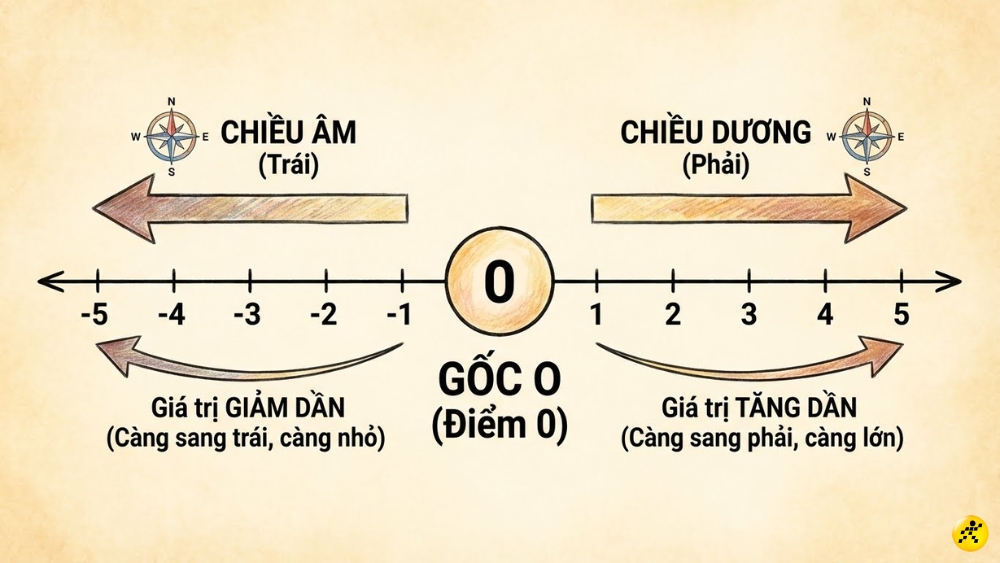
3. Biểu diễn số nguyên trên trục số

Trục số là công cụ trực quan giúp chúng ta hình dung thứ tự và khoảng cách giữa các số nguyên. Trục số thường là một đường thẳng nằm ngang với các đặc điểm sau:

• Điểm gốc: Là vị trí của số 0, nằm ở giữa trục số.
• Chiều dương: Nằm ở bên phải điểm gốc 0, biểu diễn các số nguyên dương. Càng đi về bên phải, giá trị của số càng lớn.
• Chiều âm: Nằm ở bên trái điểm gốc 0, biểu diễn các số nguyên âm. Càng đi về bên trái, giá trị của số càng nhỏ.

Nguyên tắc so sánh: Trên trục số nằm ngang, nếu số a nằm bên phải số b thì a lớn hơn b (a > b). Ví dụ, số 2 nằm bên phải số -3 nên 2 > -3. Mọi số nguyên dương đều lớn hơn số 0 và mọi số nguyên âm đều nhỏ hơn số 0.

Biểu diễn số nguyên trên trục số

4. Mối quan hệ giữa Z và các tập hợp số khác

Trong hệ thống phân loại số học, các tập hợp số có mối quan hệ bao hàm lẫn nhau. Hiểu được vị trí của Z giúp bạn xác định một số thuộc về những tập hợp nào.

• Quan hệ với tập hợp số tự nhiên (N): Mọi số tự nhiên (0, 1, 2…) đều là số nguyên. Do đó, N là tập hợp con của Z (N ⊂ Z).
• Quan hệ với tập hợp số hữu tỉ (Q): Mọi số nguyên z đều có thể viết dưới dạng phân số z/1. Vì vậy, mọi số nguyên đều là số hữu tỉ, dẫn đến Z là tập hợp con của Q (Z ⊂ Q).
• Quan hệ với tập hợp số thực (R): Số thực bao hàm cả số hữu tỉ và số vô tỉ, nên hiển nhiên Z cũng là tập hợp con của R.

Chuỗi quan hệ logic đầy đủ mà bạn nên nhớ là: N ⊂ Z ⊂ Q ⊂ R ⊂ C (với C là tập hợp số phức).

Mối quan hệ giữa Z và các tập hợp số khác

5. Các dạng bài tập về tập hợp Z kèm lời giải

Để nắm vững kiến thức về số nguyên, học sinh cần rèn luyện các dạng bài tập cơ bản sau:

Dạng bài tập	Ví dụ minh họa
Điền ký hiệu (∈, ∉, ⊂)	Điền ký hiệu thích hợp vào ô trống: -5 [ ] Z; 0.5 [ ] Z; N [ ] Z.
Tìm số đối	Tìm số đối của các số sau: 10; -7; 0.
So sánh số nguyên	Sắp xếp các số -5, 2, 0, -1 theo thứ tự tăng dần.
Liệt kê phần tử	Viết tập hợp các số nguyên x sao cho -2 < x ≤ 2.

Liệt kê phần tử

Xác định các số nguyên thỏa mãn điều kiện cho trước.

Bài tập: Viết tập hợp A = { x ∈ Z | -3 < x ≤ 2 } bằng cách liệt kê.

Lời giải: A = {-2, -1, 0, 1, 2}. Vì x nguyên nên lấy các số từ -2 đến 2.

Bất đẳng thức giá trị tuyệt đối

Tìm x ∈ Z thỏa mãn bất đẳng thức liên quan đến |x|.

Bài tập: Tìm x ∈ Z sao cho 2 < |x| ≤ 5.

Lời giải: |x| ∈ {3, 4, 5}, nên x ∈ {-5, -4, -3, 3, 4, 5}.

Phép toán tập hợp

Tính hợp, giao, hiệu của các tập con Z.

Bài tập: Cho A = { x ∈ Z | 1 ≤ x ≤ 4 }, B = { x ∈ Z | 3 ≤ x ≤ 6 }. Tính A ∩ B.

Lời giải: A = {1,2,3,4}, B = {3,4,5,6}, nên A ∩ B = {3,4}.

Thứ tự và so sánh

Xác định quan hệ thứ tự giữa các số nguyên.

Bài tập: Sắp xếp theo thứ tự tăng dần: -3, 0, 2, -1.

Lời giải: -3 < -1 < 0 < 2.

Tập hợp có tham số

Tìm m để A và B có quan hệ nhất định.

Bài tập: Tìm m ∈ Z sao cho A = { x ∈ Z | x > m } ⊆ B = { x ∈ Z | x ≥ m+2 }.

Lời giải: Không tồn tại m vì A chứa m+1 nhưng B không chứa.

6. Ứng dụng của số nguyên trong đời sống

Số nguyên hiện diện khắp nơi trong đời sống thực tế, giúp con người mô tả các trạng thái đối lập một cách chính xác.

• Nhiệt độ: Các vùng khí hậu lạnh thường có nhiệt độ dưới 0 độ C, được biểu thị bằng số nguyên âm (ví dụ: -10 độ C).
• Độ cao địa lý: Người ta dùng số 0 để chỉ mực nước biển. Độ cao của đỉnh núi được biểu thị bằng số dương, trong khi độ sâu dưới mực nước biển được biểu thị bằng số âm.
• Tài chính: Trong kế toán, số dương biểu thị số dư hoặc lợi nhuận, còn số nguyên âm biểu thị khoản nợ hoặc thâm hụt ngân sách.
• Thời gian: Trong lịch sử các năm trước Công nguyên tương ứng với giá trị âm trên dòng thời gian.

Ứng dụng của số nguyên trong đời sống

7. Các câu hỏi liên quan về tập hợp Z

Số 0 có thuộc tập hợp Z không?

Số 0 có thuộc tập hợp Z. Nó đóng vai trò là ranh giới giữa tập hợp số nguyên dương và tập hợp số nguyên âm.

Số thập phân có phải là số nguyên không?

Số thập phân không phải là số nguyên. Các số như 1.5, 2.75 hoặc -3.14 không phải là số nguyên.

Số nguyên phải là những số không có phần dư hay phần thập phân.

Tại sao tập hợp số nguyên không dùng ký hiệu I mà là dùng Z?

Mặc dù trong tiếng Anh số nguyên là “Integer”, nhưng ký hiệu Z đã được quốc tế hóa dựa trên tiếng Đức “Zahlen” để tránh nhầm lẫn với các ký hiệu khác trong toán học như I (thường dùng cho số vô tỉ).

Tập hợp Z* khác gì so với tập hợp Z?

Tập hợp Z* là tập hợp các số nguyên bỏ đi phần tử 0. Trong khi Z chứa số 0, thì Z* chỉ chứa các số nguyên âm và số nguyên dương.

Khám phá thêm các mẫu laptop mạnh mẽ để hỗ trợ việc cài đặt phần mềm toán học và nghiên cứu:

Hy vọng bài viết này đã giúp bạn hiểu rõ Z là tập hợp số gì cũng như nắm vững các tính chất cơ bản của số nguyên. Chúc bạn có những giờ học toán thật thú vị và đạt kết quả cao nhé!